퍼셉트론(Perceptron) 이란?
퍼셉트론은 신경망의 기원이 되는 알고리즘으로 '다수의 신호를 입력받아 하나의 신호를 출력하는 것' 이다. 은닉층이 없고 매개변수를 스스로 조정 할 수 없어 신경망 이라고 할 수 는 없다. 하지만 신경망을 이루는 가장 기본적인 컨셉이자 요소가 된다. 단순 퍼셉트론(SLP, Single-Layer Perceptron) 이라고도 한다.
퍼셉트론(Perceptron) 의 구조
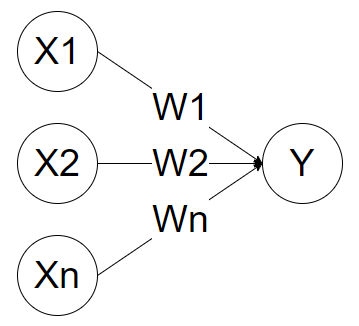
퍼셉트론은 다수의 입력신호(X1,X2 ... Xn), 입력신호 별 가중치(Weight), 출력신호(Y)로 이루어져 있고 각각의 원은 뉴런, 또는 노드 라고 부른다. 출력신호는 '신호가 흐른다(1)' 혹은 '신호가 흐르지 않는다(0)' 의 두가지 값을 가질 수 있는데 입력신호들이 가중치를 거쳐 보낸 값이 정해진 한계값을 넘으면 1, 그렇지 않으면 0을 출력한다. 여기서 정해진 값은 임계값(threshold)이라고 하며 θ(theta) 기호로 표기한다.
하나의 입력 노드에서 출력노드로 흐를때 입력 노드의 값에 각각의 고유한 가중치가 곱해져서 보내진다. 출력 노드는 입력노드들로 부터 받은 X*W 값의 합이 임계값보다 높은지 낮은지를 판단하여 뉴런을 활성화(출력값이 1) 한다. 따라서 아래와 같은 수식으로 표현 할 수 있다.
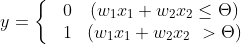
가중치(Weight)
가중치는 각 입력노드가 출력노드에 끼치는 영향력을 조절하는 요소이다. 가중치가 크다면 해당하는 입력노드가 출력노드를 결정하는 중요한 신호라는 것을 의미한다. 아래의 예시는 입력신호와 각 가중치의 곱의 합이 임계값을 넘지 못해 출력신호가 활성화 되지 못한 퍼셉트론이다.
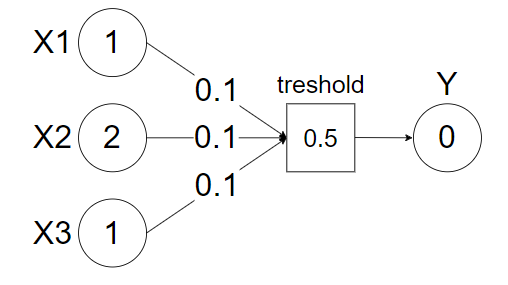
우리가 위의 퍼셉트론의 출력신호가 활성화 되는 결과를 원한다고 할때 가중치 값을 수정하여 해결할 수 있다. 아래 그림과 같다.

위의 그림은 X1의 가중치 W1의 값을 0.1에서 0.3으로 수정하여 출력신호 Y를 활성화 시킨 예이다. 이때 가중치 W1의 값이 커졌다는 것은 입력신호 X1의 영향력이 커졌다라고 말 할 수 있다. 위와 같이 가중치의 값을 줄이고 늘리며 각 입력신호의 영향력을 조절하여 원하는 출력신호의 값을 얻을 수 있다. 결론적으로 가중치는 입력신호가 출력신호에 미치는 영향도 이고, 하나의 출력신호를 우리가 원하는 방향으로 출력시키기 위해(활성화 또는 비활성화) 사용자가 임의로 지정하고 변경하는 값(hyper parameter) 이다.
활성화 함수(Activation function)와 편향(Bios)
위에서 우리는 아래와 같은 식으로 퍼셉트론을 표현 하였다.
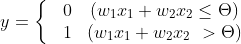
위의 식에서 임계값(θ) 을 -b라는 기호로 치환하여 부등호 왼쪽으로 넘기면 아래와 같이 표현이 가능하다.
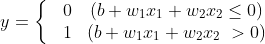
이 때에 다소 복잡해 보이는 식들을 함수 h를 이용하여 표현하면 아래와 같이 쓸 수 있다.

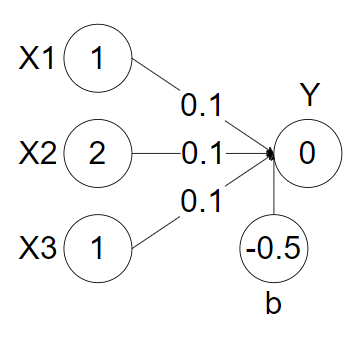
이 때, h(x) 는 활성화 함수 라고 하며 b는 - 임계값(θ) 으로 '편향'(bios) 라고 한다. 즉, 활성화 함수는 입력신호의 총합을 출력신호로 변환하는 함수를 말하는데 자세한 내용은 다음 포스팅([ML-T][NN-B] 02. 활성화(Activation) 함수) 에서 다루겠다. (위의 활성화 함수는 계단함수로 표현되어 있다.) 편향은 출력노드가 얼마나 쉽게 활성화 되느냐를 조정하는 요소이다. 아래 이미지는 입력신호와 가중치의 곱의 합은 0을 넘지만 편향으로 인해 출력 신호를 활성화 시키지 못한 퍼셉트론의 예시이다.
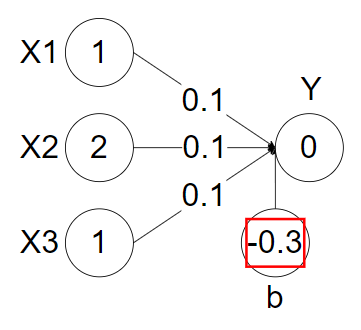
위와 같이 편향이 작아 질 수록 결국 임계값이 커지는 것 이므로 퍼셉트론을 활성화 시키기 쉽지 않다. 우리가 편향을 수정하여 위의 출력신호를 활성화 시키고자 한다면 아래 이미지와 같이 편향 값을 조정해야 한다.
결론적으로 편향은 출력신호를 얼마나 쉽게 활성화 시키는지 기준이 되는 변수이고, 하나의 출력신호를 우리가 원하는 방향으로 출력시키기 위해(활성화 또는 비활성화) 사용자가 임의로 지정하고 변경하는 값(hyper parameter) 이다.
순전파(Forward Propagation)
순전파란 입력층부터 출력층까지 순서대로 데이터를 계산하고 저장하는 것을 말한다. 퍼셉트론은 순전파를 진행하여 입력층과 가중치, 편향의 값을 활성화 함수를 거쳐 출력층으로 보낸다.
단순 퍼셉트론(SLP, Single-Layer Perceptron)의 한계
- 비선형 구조의 문제를 해결 할 수 없다.
단순 퍼셉트론은 AND, NAND, OR 게이트의 문제는 풀수 있지만 XOR 게이트의 문제를 풀 수 없다. 즉, 선형 문제는 구분할 수 있으나 아래와 같은 비선형 구조의 문제를 해결 할 수 없다.
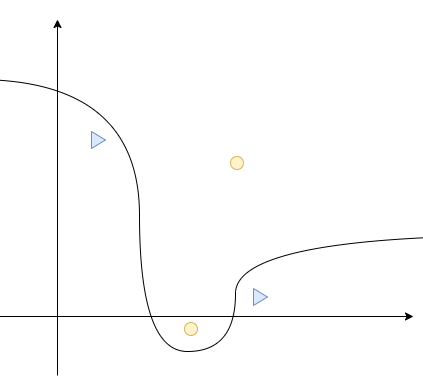
- 가중치와 편향이 Hyper parameter 이다.
가중치는 입력신호가 많아질 수록 점점 늘어나는 매개 변수 이다. 위에서 설명했던 다층 퍼셉트론을 적용하면 가중치와 더불어 편향의 갯수 또한 늘어나게 되는데 이것을 사람이 수동으로 적절한 값을 찾아 조정하는 것은 굉장히 번거로운 과정이다.
※ 해결 방법 : 신경망(Neural Network)
신경망은 다층 퍼셉트론의 형태를 가져 비선형 영역의 문제를 해결 할 수 있다. 더하여 순전파 만을 진행했던 퍼셉트론과 달리 '오차역전파'를 통해 가중치와 편향 또한 자동으로 조정 할 수 있는 특성을 가진다.
'Machine Learning(이론) > NN(Neural network)(Basic)' 카테고리의 다른 글
| [ML-T][NN-B] 02. 다층 퍼셉트론(MLP, Multi-Layer Perceptron) (0) | 2021.11.05 |
|---|---|
| [ML-T][NN-B] 03. 활성화(Activation) 함수 (0) | 2021.10.16 |
| [ML-t][MLP] (02) 오차역전파(Error Backpropagation) 구현 - 회귀모델 (0) | 2021.10.10 |
| [ML-t][MLP](01) 오차역전파(Error Backpropagation) 이론 (0) | 2021.10.10 |
| [ML-T][NN-B] 00. Intro (0) | 2021.10.10 |


